以下题目均来自leetcode、poj
岛屿数量
给定一个由 ’1’(陆地)和 ‘0’(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例 1:
输入: 11110 11010 11000 00000
输出: 1 示例 2:
输入: 11000 11000 00100 00011
输出: 3
class Solution {
private:
void DFS(std::vector<std::vector<int>> &mark,
std::vector<std::vector<char>> &grid,int x,int y){
static const int dx[] = {-1,1,0,0};
static const int dy[] = {0,0,-1,1};
mark[x][y] = 1;
for(int i = 0;i < 4;i++){
int newx = x+dx[i];
int newy = y+dx[j];
if(newx < 0 || newx > mark.size() ||
newy < 0 || newy > mark[newx].size() ||
){
continue;
}
if(mark[newx][newy] == 0 && grid[newx][newy] == '1'){
DFS(mark,grind,newx,newy);
}
}
}
void BFS(std::vector<std::vector<int>> &mark,
std::vector<std::vector<char>> &grid,int x,int y){
static const int dx[] = {-1,1,0,0};
static const int dy[] = {0,0,-1,1};
mark[x][y] = 1;
std::queue<std::pair<int,int>> q;
q.push(std::make_pair(x,y));
while(!q.empty()){
x = q.front().first;
y = q.front().second;
q.pop();
for(int i = 0;i < 4;i++){
int newx = x+dx[i];
int newy = y+dx[j];
if(newx < 0 || newx > mark.size() ||
newy < 0 || newy > mark[newx].size() ||
){
continue;
}
if(mark[newx][newy] == 0 && grid[newx][newy] == '1'){
q.push(std::make_pair(newx,newy));
mark[newx][newy] = 1;
}
}
}
}
public:
int numIslands(vector<vector<char>>& grid) {
int islandNum = 0;
std::vector<std::vector<int>> mark;
for(int i = 0;i < grid.size();i++){
mark.push_back(std::vector<int>());
for(int j = 0;j < grid[i].size();j++){
mark[i].push_back(0);
}
}
for(int i = 0;i < grid.size();i++){
mark.push_back(std::vector<int>());
for(int j = 0;j < grid[i].size();j++){
if(grid[i][j] == '1' && mark[i][j] == 0){
DFS(mark,grid,i,j);
islandNum++;
}
}
}
return islandNum;
}
};
单词接龙
给定两个单词(beginWord 和 endWord)和一个字典,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
每次转换只能改变一个字母。 转换过程中的中间单词必须是字典中的单词。 说明:
如果不存在这样的转换序列,返回 0。 所有单词具有相同的长度。 所有单词只由小写字母组成。 字典中不存在重复的单词。 你可以假设 beginWord 和 endWord 是非空的,且二者不相同。 示例 1:
输入: beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]
输出: 5
解释: 一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。 示例 2:
输入: beginWord = “hit” endWord = “cog” wordList = [“hot”,”dot”,”dog”,”lot”,”log”]
输出: 0
解释: endWord “cog” 不在字典中,所以无法进行转换。
class Solution {
private:
bool connect(const string& word1, const string& word2){
int cnt = 0;
for (int i = 0;i < word1.length(); i++){
if(word1[i] != word2[i]){
cnt++;
}
}
return cnt == 1;
}
void makeGraph(std::string& beginWord,std::vector<std::string>& wordList,std::map<std::string,std::vector<std::string> &graph){
wordList.push_back(beginWord);
for (int i = 0;i < wordList.size(); i++){
graph[wordList[i]] = std::vector<std::string>();
}
for(int i = 0;i < wordList.size(); i++){
for (int j = i+1;j < wordList.size(); j++){
if(connect[wordList[i],wordList[j])){
graph[wordList[i].push_back(wordList[j])];
graph[wordList[j].push_back(wordList[i])];
}
}
}
}
int BFSGraph(string& beginWord, string& endWord, std::map<std::string,std::vector<std::string> &graph) {
std::queue<std::pair<std::string,int>> q;
std::set<std::string> visit;
q.push(std::make_pair(beginWord,1));
visit.insert(beginWord);
while(!q.empty()){
std::string node = q.front().first;
int step = q.front().second;
q.pop();
if(node == endWord){
return step;
}
const std::vector<std::string>& neighbors = graph[node];
for(int i = 0; i < neighbors.size(); i++){
if(visit.find(neighbors[i]) == visit.end()){
q.push(std::make_pair(neighbors[i],step+1));
visit.insert(neighbors[i]);
}
}
}
return 0;
}
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
std::map<std::string,std::vector<std::string> graph;
makeGraph(beginWord,wordList,graph);
return BFSGraph(beginWord,endWord,graph);
}
};
单词接龙 II
给定两个单词(beginWord 和 endWord)和一个字典 wordList,找出所有从 beginWord 到 endWord 的最短转换序列。转换需遵循如下规则:
每次转换只能改变一个字母。 转换过程中的中间单词必须是字典中的单词。 说明:
如果不存在这样的转换序列,返回一个空列表。 所有单词具有相同的长度。 所有单词只由小写字母组成。 字典中不存在重复的单词。 你可以假设 beginWord 和 endWord 是非空的,且二者不相同。 示例 1:
输入: beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]
输出: [ [“hit”,”hot”,”dot”,”dog”,”cog”], [“hit”,”hot”,”lot”,”log”,”cog”] ] 示例 2:
输入: beginWord = “hit” endWord = “cog” wordList = [“hot”,”dot”,”dog”,”lot”,”log”]
输出: []
解释: endWord “cog” 不在字典中,所以不存在符合要求的转换序列。
struct Qitem{
std::string node;
int parent_pos;
int step;
Qitem(std::string node, int parent_pos, int step):node(node),parent_pos(parent_pos),step(step){}
};
class Solution {
private:
void makeGraph(std::string& beginWord,std::vector<std::string>& wordList,std::map<std::string,std::vector<std::string> &graph){
//wordList里可能有beginWord
int has_begin_word = 0;
for (int i = 0;i < wordList.size(); i++){
if(wordList[i] == beginWord){
has_begin_word = 1;i
}
graph[wordList[i]] = std::vector<std::string>();
}
for(int i = 0;i < wordList.size(); i++){
for (int j = i+1;j < wordList.size(); j++){
if(connect[wordList[i],wordList[j])){
graph[wordList[i].push_back(wordList[j])];
graph[wordList[j].push_back(wordList[i])];
}
if(has_begin_word == 0 && connect(beginWord,wordList[i])){
graph[beginWord].push_back(wordList[i]);
}
}
}
}
void BFSGraph(string& beginWord, string& endWord, std::map<std::string,std::vector<std::string> &graph,
std::vector<Qitem>>&Q,
std::vector<int>& endWordPos){
std::map<std::string,int> visit;
int minStep = 0;
q.push_back(Qitem(beginWord.c_str(), -1,1));
visit[beginWord] = 1;
int front = 0;
while(front != q.size()){
const std::string &node = q.front().first;
int step = q[front].step;
if(minStep != 0 && step > minStep){
break;
}
if(node == endWord){
minStep = step;
endWordPos.push_back(front);
}
const std::vector<std::string>& neighbors = graph[node];
for(int i = 0; i < neighbors.size(); i++){
//节点未访问到,或另外一条最短路径
if(visit.find(neighbors[i]) == visit.end() || visit[neighbors[i]] = step + 1){
q.push(Qitem(neighbors[i],front,step+1));
visit[neighbors[i]] = step + 1;
}
}
front++;
}
}
public:
vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
std::map<std::string,std::vector<std::string> graph;
makeGraph(beginWord,wordList,graph);
std::vector<Qitem> q;
std::vector<int> endWordPos;
BFSGraph(beginWord,endWord,graph,q,endWordPos);
std::vector<std::vector<std::string>> result;
for (int i = 0; i < endWordPos.size();i++){
int pos = endWordPos[i];
std::vector<std::string> path;
while(pos != -1){
path.push_back(q[pos].node);
pos = q[pos].parent_pos;
}
result.push_back(std::vector<std::string>());
for(int j = path.size() - 1; j >= 0; j--){
result[i].push_back(path[j]);
}
}
return result;
}
};
火柴拼正方形
还记得童话《卖火柴的小女孩》吗?现在,你知道小女孩有多少根火柴,请找出一种能使用所有火柴拼成一个正方形的方法。不能折断火柴,可以把火柴连接起来,并且每根火柴都要用到。
输入为小女孩拥有火柴的数目,每根火柴用其长度表示。输出即为是否能用所有的火柴拼成正方形。
示例 1:
输入: [1,1,2,2,2] 输出: true
解释: 能拼成一个边长为2的正方形,每边两根火柴。 示例 2:
输入: [3,3,3,3,4] 输出: false
解释: 不能用所有火柴拼成一个正方形。 注意:
给定的火柴长度和在 0 到 10^9之间。 火柴数组的长度不超过15。
class Solution {
public:
bool makesquare(vector<int>& nums) {
if(nums.size() < 4){
return false;
}
int sum = 0;
for(int i = 0; i < nums.size;i++){
sum += nums[i];
}
if(sum%4 != 0){
return false;
}
std::sort(nums.begin(),nums.end());
int bucket[4] = {0};
return generate(0,nums,sum/4,bucket);
}
private:
bool generate(int i,std::vector<int>& nums,int traget,int bucket[]){
if(i >= nums.size()){
return bucket[0] == traget && bucket[1] == traget && bucket[2] == traget && bucket[3] == traget;
}
for(int j = 0;j < 4;j++){
if(bucket[j] + nums[i] > target){
continue;
}
bucket[j] += nums[i];
if(generate(i + 1,nums,target,bucket)){
return true;
}
bucket[j] -= nums[i];
}
return false;
}
};
接雨水 II
给定一个 m x n 的矩阵,其中的值均为正整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。
说明:
m 和 n 都是小于110的整数。每一个单位的高度都大于 0 且小于 20000。
示例:
给出如下 3x6 的高度图: [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ]
返回 4。
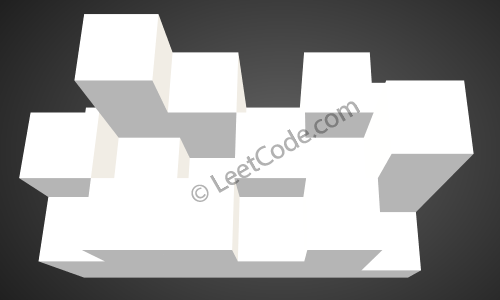
如上图所示,这是下雨前的高度图[[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] 的状态。
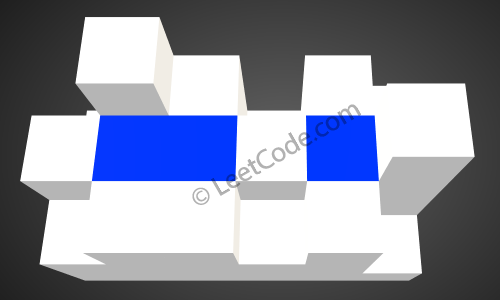
下雨后,雨水将会被存储在这些方块中。总的接雨水量是4。
struct Qitem{
int x;
int y;
int h;
Qitem(int x, int y, int h):x(x),y(y),h(h){}
};
class Solution {
public:
int trapRainWater(vector<vector<int>>& heightMap) {
std::priority_queue<Qitem,std::vector<Qitem>,cmp> q;
if (heightMap.size() < 3 || heightMap[0].size() < 3){
return 0;
}
int row = heightMap.size();
int col = heightMap[0].size();
std::vector<std::vector<int>> mark;
for (int i = 0; i < row;i++){
mark.push_back(std::vector<int>());
for (int j = 0; j < col;j++){
mark[i].push_back(0);
}
}
//优先放入四周到q
for(int i = 0; i < row;i++){
q.push(Qitem(i,0,heightMap[i][0]));
mark[i][0] = 1;
q.push(Qitem(i,column - 1,heightMap[i][column - 1]));
mark[i][column - 1] = 1;
}
for(int i = 1; i < column - 1;i++){
q.push(Qitem(i,0,heightMap[0][i]));
mark[0][i] = 1;
q.push(Qitem(row - 1,i,heightMap[row - 1][i]));
mark[row - 1][i] = 1;
}
static const int dx[] = {-1,1,0,0};
static const int dy[] = {0,0,-1,1};
int result = 0;
while(!q.empty()){
int x = q.top().x;
int y = q.top().y;
int h = q.top().h;
q.pop();
for(int i = 0;i < 4;i++){
int newx = x+dx[i];
int newy = y+dy[i];
if(newx < 0 || newx >= row) || newy < 0 || newy >= column || mark[newx][newy]){
continue;
}
if(h > heightMap[newx][newy]){ //灌水超过进入点
result += h - heightMap[newx][newy];
heightMap[newx][newy] = h;
}
q.push(Qitem(newx,newy,heightMap[newx][newy]));
mark[newx][newy] = 1;
}
}
return result;
}
};