正交投影
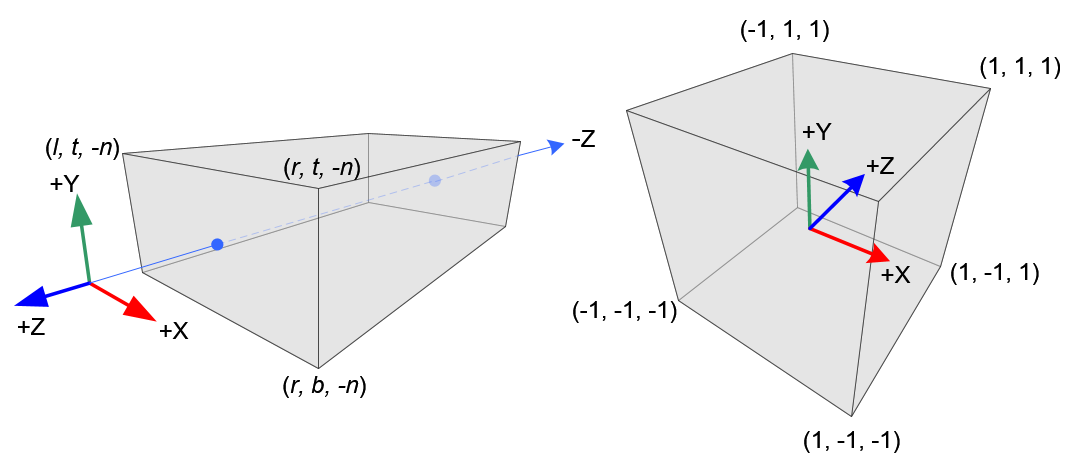
观察坐标为右手坐标系,NDC使用左手坐标系。定义屏幕左右边界为left和right 屏幕上下边界为top和bottom,近的裁剪面距离为n,远的裁剪面距离为f。
观察空间的x_eye、y_eye与z_eye分量都线性映射到NDC。我们只需将长方体缩放为正方体,然后移动它到原点。让我们使用线性关系推导所有元素。
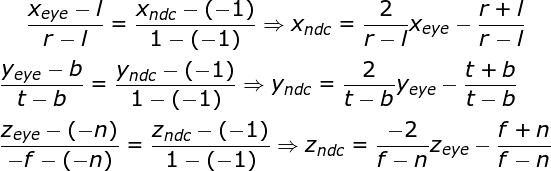
投影矩阵:一个缩放和平移矩阵结合。
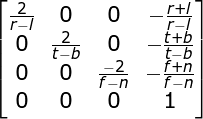
Unity源码实现
m_ProjectionMatrix.SetOrtho( -m_OrthographicSize * m_Aspect, m_OrthographicSize * m_Aspect, -m_OrthographicSize, m_OrthographicSize, m_NearClip, m_FarClip );
Matrix4x4f& Matrix4x4f::SetOrtho (
float left,
float right,
float bottom,
float top,
float zNear,
float zFar )
{
SetIdentity ();
float deltax = right - left;
float deltay = top - bottom;
float deltaz = zFar - zNear;
Get(0,0) = 2.0F / deltax;
Get(0,3) = -(right + left) / deltax;
Get(1,1) = 2.0F / deltay;
Get(1,3) = -(top + bottom) / deltay;
Get(2,2) = -2.0F / deltaz;
Get(2,3) = -(zFar + zNear) / deltaz;
return *this;
}
透视投影
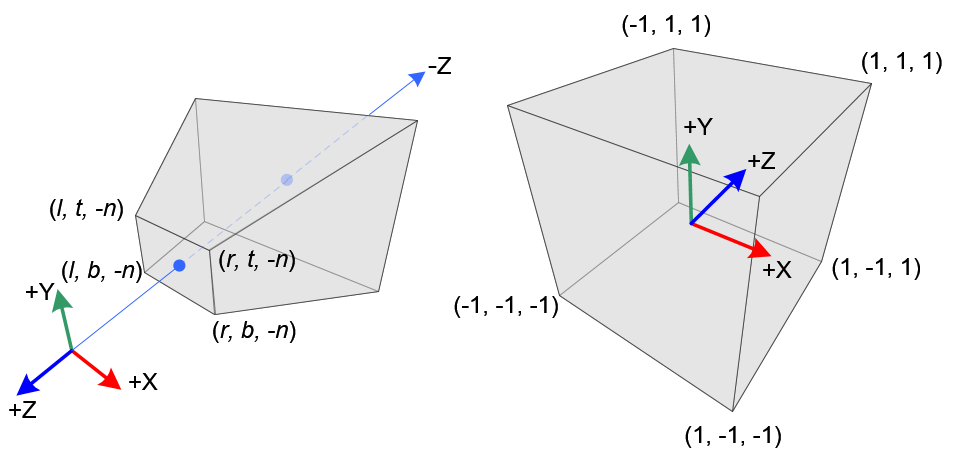
在透视投影中,观察坐标中的3D点会被映射到立方体(NDC:Normalized Device Coordinates )中。x坐标的范围从[l,f]到[-1,1],y坐标的范围从[b,t]到[-1,1],z坐标的范围从[n,f]到[-1,1]。
下图显示了观察坐标中的点(x_eye,y_eye,z_eye)如何投影到近平面上的(x_p,y_p,z_p),其通过使用相似三角形的比率来计算。
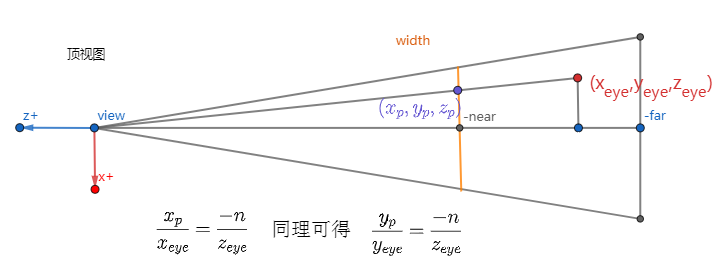
投影的结果z_p始终等于-n,在投影面上。实际上,z_p对于投影后的p=(-nx_eye/z_eye,-ny_eye/z_eye,-n)已经没有意义了,这个信息点已经没用了。但对于3D图形管线来说,为了便于进行后面的片元操作,例如z缓冲消隐算法,有必要把投影之前的z保存下来,方便后面使用。注意,x_p和y_p都取决于z_eye ; 它们与-z_eye成反比。换句话说,它们都被-z_eye除以。
在通过乘以投影矩阵变换观察坐标之后,剪辑坐标仍然是齐次坐标。它最终变为归一化设备坐标(NDC)除以剪辑坐标的w分量,w_clip = -z_eye.
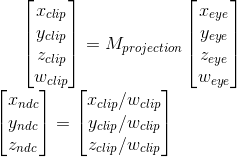
如上正交投影推导一样x_p和y_p映射到具有线性关系的NDC的x_ndc和y_ndc有如下二式。
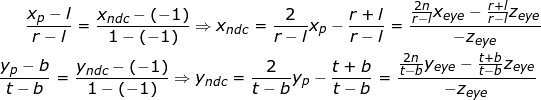
推出下列矩阵:
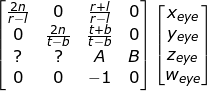
z不依赖于x或y值,因此我们借用w分量来找到z_ndc和z_eye之间的关系,在观察空间中,w_eye等于1:
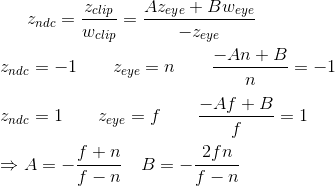
最后得出透视投影矩阵,它是通用的,左右两边不对称。投影点不在屏幕中心点。
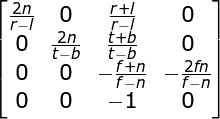
Unity中源码实现为:
Matrix4x4f& Matrix4x4f::SetFrustum (
float left,
float right,
float bottom,
float top,
float nearval,
float farval )
{
float x, y, a, b, c, d, e;
x = (2.0F * nearval) / (right - left);
y = (2.0F * nearval) / (top - bottom);
a = (right + left) / (right - left);
b = (top + bottom) / (top - bottom);
c = -(farval + nearval) / (farval - nearval);
d = -(2.0f * farval * nearval) / (farval - nearval);
e = -1.0f;
Get (0,0) = x; Get (0,1) = 0.0; Get (0,2) = a; Get (0,3) = 0.0;
Get (1,0) = 0.0; Get (1,1) = y; Get (1,2) = b; Get (1,3) = 0.0;
Get (2,0) = 0.0; Get (2,1) = 0.0; Get (2,2) = c; Get (2,3) = d;
Get (3,0) = 0.0; Get (3,1) = 0.0; Get (3,2) = e; Get (3,3) = 0.0;
return *this;
}
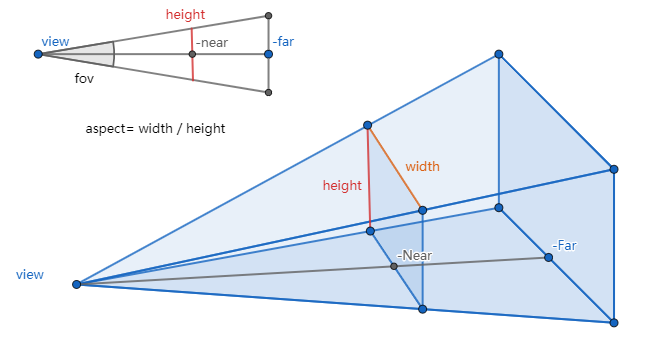
而unity editor中使用的fov和aspect来处理相机。
-
fov是视景体竖直方向上的张角,如侧视图所示。
-
aspect等于width / height,是照相机水平方向和竖直方向长度的比值。
-
near和far分别是照相机到视景体最近、最远的距离,均为正值,且far应大于near。
当上图椎体对称时,其 right left 大小相同 一正一负,投影点正好在屏幕中心点
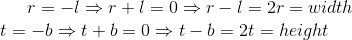
投影矩阵简化为:
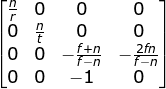
再带入二个fov和aspect系数:
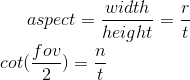
得出Unity使用的透视投影矩阵,
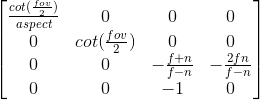
Unity中源码实现为:
m_ProjectionMatrix.SetPerspective( m_FieldOfView, m_Aspect, m_NearClip, m_FarClip );
Matrix4x4f& Matrix4x4f::SetPerspective(
float fovy,
float aspect,
float zNear,
float zFar )
{
float cotangent, deltaZ;
float radians = Deg2Rad (fovy / 2.0f);
cotangent = cos (radians) / sin (radians);
deltaZ = zNear - zFar;
Get (0,0) = cotangent / aspect; Get (0,1) = 0.0F; Get (0,2) = 0.0F; Get (0,3) = 0.0F;
Get (1,0) = 0.0F; Get (1,1) = cotangent; Get (1,2) = 0.0F; Get (1,3) = 0.0F;
Get (2,0) = 0.0F; Get (2,1) = 0.0F; Get (2,2) = (zFar + zNear) / deltaZ; Get (2,3) = 2.0F * zNear * zFar / deltaZ;
Get (3,0) = 0.0F; Get (3,1) = 0.0F; Get (3,2) = -1.0F; Get (3,3) = 0.0F;
return *this;
}
canonical view volume(规则观察体)
CVV:Canonical View Volume(规则观察体),上面推导的变换最终的坐标应该是NDC的,但是为了更方便地做一些其他的操作,主要是CVV裁剪,引入了一个新的空间,这个空间主要是没有NDC空间的坐标没进行除以w计算,也就是说CVV空间的顶点还是齐次空间下的,除了w之后才会变为NDC空间,两者的差距主要是是否除以了w。
NDC:Normalized Device Coordinates(标准设备空间),通过齐次除法(homogeneous division )也叫透视除法(Perspective division)把齐次裁剪坐标空间转化到NDC(普通坐标)中。因为渲染设备分辨率有差异,在做一些计算处理时,没办法根据分辨率进行调整,而通过这样一个空间,把x,y映射到(-1,1)区间,z映射到(-1,1)区间(Unity选用OpenGL这样的齐次裁剪空间,其区间是(-1,1),而DirectX是(0,1)),在下一步屏幕坐标映射时再根据屏幕分辨率生成像素真正应该在的位置,这样可以避免了设备适配的问题。
参考资料: