What You See Is What You Get
基于物理渲染

这不是照片,而是来自SubStance物理渲染效果。
BRDF模型
来自度娘的定义:双向反射分布函数(Bidirectional Reflectance Distribution Function,BRDF)用来定义给定入射方向上的辐射照度(irradiance)如何影响给定出射方向上的辐射率(radiance)
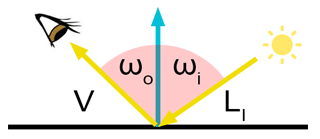
BRDF例子
BRDF的数值模型分为三类
- 经验模型(Empirical Models):使用基于实验提出的公式对BRDF做快速估计
-
Lambert模型,通过常数BRDF表示完美的漫反射(无光泽)表面。
-
Phong模型,一种类似塑料镜面反射的现象学模型。
-
Blinn-Phong模型,类似Phong,但允许插量,减少计算开销。
- 基于物理的模型(Physical-based Models):根据物体表面材料的几何以及光学属性简易反射方程计算BRDF
-
Torrance-Sparrow模型,表示表面为完全镜面微平面的分布的一般模型。
-
Cook-Torrance模型,一种镜面微平面模型(Torrance-Sparrow),它考虑了波长,从而影响色移。
-
Ward模型,具有椭圆 - 高斯分布函数的镜面 - 微平面模型,取决于表面切线方向(除表面法线外)。
-
Oren-Nayar模型,一种“定向漫射”微平面模型,具有完美的漫射(而非镜面)微平面。
-
Ashikhmin- Shirley模型,允许各向异性反射,以及镜面下的漫射基板。
-
HTSG(He,Torrance,Sillion,Greenberg),一个全面的物理模型。
- 数据表达的模型(Data-driven Models):将BRDF按照实测数据建立查找表,以便于快速的查找和计算
-
适合Lafortune模型,具有多个镜面波瓣的Phong的推广,用于测量数据的参数拟合。
-
用于分析网格BRDF近似的Lebedev模型。
基础数学知识
球面坐标(Spherical Coordinate)
球面坐标比用向量描述光线更方便。
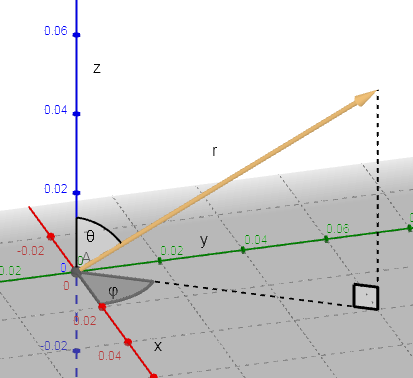
球面坐标中的向量表示如下
-
r表示向量长度
-
θ表示向量与z轴的夹角
-
φ表示向量在x-y平面上的投影与x轴逆时针夹角
笛卡尔坐标向球面坐标转换
r = sqrt(x^2 + y^2 + z^2)
θ = acos(z/r)
φ = atan2(y/x)
x = rsinθcosφ
y = rsinθsinφ
z = rcosφ
立体角(Solid Angel)
光一般从一个以立体角表示的方向范围到达或离开表面点。
在二维平面上,一个圆的圆弧的微分记为ds(也叫弧微分),半径为r,则圆心角指的是弧微分与半径的比值:dθ=ds/r,对这个式子做0到2π的积分的话,显然右边的分子变成了圆周长2πr,圆心角为2πr/r=2π。
立体角的da的含义是球面上的微分面积,而分母需要变成半径r的平方(1球面度所对应的立体角所对应的球面表面积为r^2 )。立体角微分形式dω = dA / ( r^2 ),球体表面积等于4πr^2,积分到整个球体,立体角的最大值等于4π,表示为整个球面。
为了画出下图研究好久GeoGebra软件,透明蓝色面积部分还是PS画上去的。
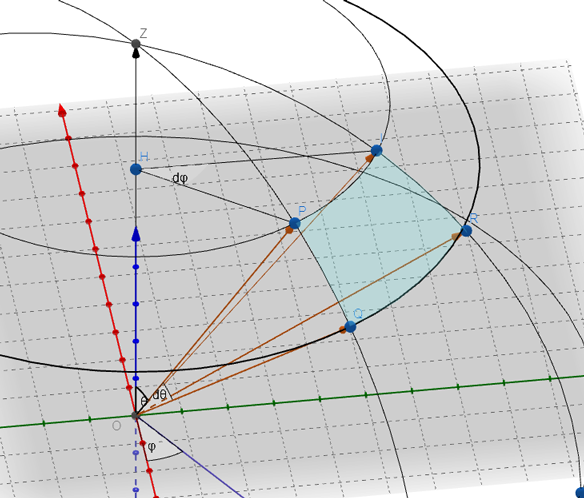
对于在θ,φ方向描述的微分立体角dθ,dφ
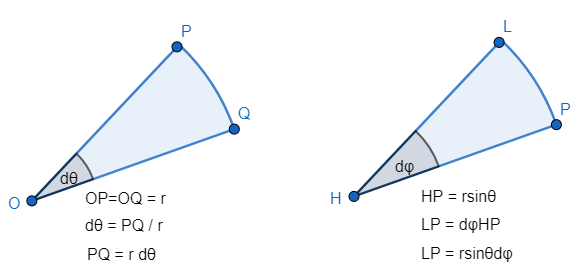
其在球面上的微分面积dA为
dA = PQ*LP
dA = (rsinθdφ)(rdθ) = r^2(sinθdθdφ)
dω = dA / ( r^2 ) = sinθdθdφ
投影面积(Foreshortened Area)
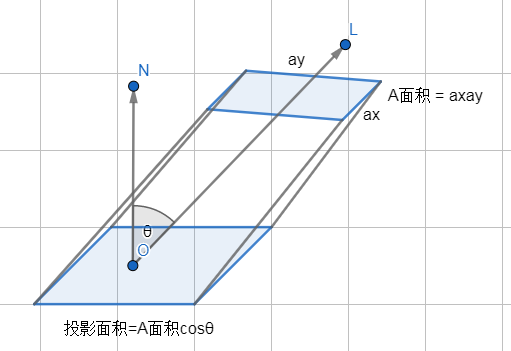
对于面积A,则沿着与法向夹角为θ方向的A的可见面积为:Acosθ
辐射度量
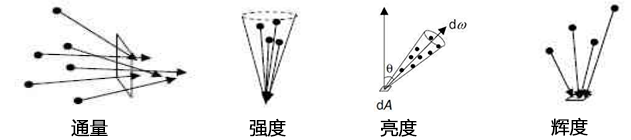
-
辐射通量/光通量 Radiant Flux : 描述的是在单位时间穿过截面的光能
-
辐射强度/发光强度 Radiant Intensity:表示每单位立体角的辐射通量
-
辐射率/光亮度 Radiance:表示物体表面沿某一方向的明亮程度,它等于每单位投影面积和单位立体角上的辐射通量。
-
辐照度/辉度 Irradiance :指入射表面的辐射通量,即单位时间内到达单位面积的辐射通量
Specular BRDF
这里选用的Cook-Torrance 近似微表面(microfacet)模型框架,有F G D 三个近似方程。
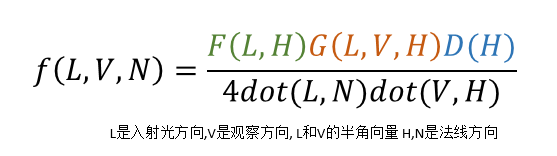
F-菲涅尔函数(Fresnel Function)
 图片来自reflection-refraction-fresnel
图片来自reflection-refraction-fresnel
当直视水(正常入射)时,你可以透过水面看到。然而,当在远处观察时(在掠射角处,感知到的光线与表面平行),您将看到水面上的镜面反射变得更加强烈。
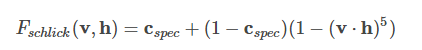
//廉价近似方程
float3 SchlickFresnelFunction(float3 F0,float VdotH){
return F0 + (1 - F0)* pow(clamp(1.0-VdotH, 0.0, 1.0),5.0);
}
//Unity中只用4次方简化
// approximage Schlick with ^4 instead of ^5
inline half3 FresnelLerpFast (half3 F0, half3 F90, half cosA)
{
half t = Pow4 (1 - cosA);
return lerp (F0, F90, t);
}
反射的光量不仅取决于视角,还取决于材料的折射率(Index Of Refraction)。在垂直入射(垂直于表面或0°角)时,反射回的光量并且可以从IOR中得出。注意到在掠射角处反射回的光量接近100%。
float SchlickIORFresnelFunction(float ior,float LdotH){
float f0 = pow((ior-1)/(ior+1),2);
return f0 + (1 - f0) * pow(clamp(1.0-LdotH, 0.0, 1.0),5.0);
}
GSF-几何阴影函数(Geometric Shadowing Function)
描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候,平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
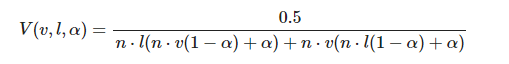
选用Smith Joint Masking-Shadowing Function,Unity中粗糙度定义α = (Roughness)^2,平滑度和粗糙度转化:Roughness=1−Smoothness
float SchlickGGXGeometricShadowingFunction (float NdotL, float NdotV, float roughness){
float k = roughness / 2;
float SmithL = (NdotL)/ (NdotL * (1- k) + k);
float SmithV = (NdotV)/ (NdotV * (1- k) + k);
float Gs = (SmithL * SmithV);
return Gs;
}
NDF-微表面分布函数(Normal Distribution Function)
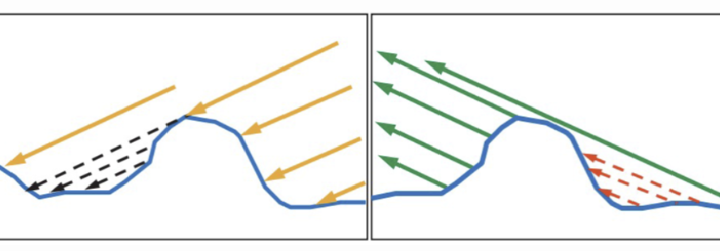
估算在受到表面粗糙度的影响下,取向方向与中间向量一致的微平面的数量。这是用来估算微平面的主要函数。
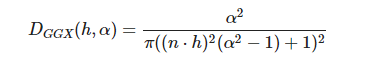
选用GGX (Trowbridge-Reitz)
float GGXNormalDistribution(float roughness, float NdotH)
{
fixed a = roughness*roughness;
fixed a2 = a*a;
fixed k = (NdotH*NdotH * (a2 - 1.0) + 1.0);
return a2 / (UNITY_PI * k * k);
}
点击查看完整的Shader和Unity2018工程(代码收集整理来自网络)
Unity内置PBR材质
Unity内置PBR模型可访问Unity\Editor\Data\CGIncludes\UnityStandardBRDF.cginc
Unity内置PBR用了三套模型:
BRDF1_Unity_PBS()
-
D: GGX or Normalized BlinnPhon
-
G: Smith Joint or Smith Beckmann
-
F: Schlick approximation
BRDF2_Unity_PBS()
-
D: BlinnPhong or [Modified] GGX
-
G: Modified Kelemen and Szirmay-Kalos
-
F: Fresnel approximated with 1/LdotH
BRDF3_Unity_PBS()
-
D: Normalized BlinnPhong in RDF form
-
G: Implicit Visibility term
-
F: No Fresnel term
Unity传统工作流
diffuse mapping 颜色贴图 + specular map 高光贴图 + normal map 法线贴图
SubStance工作流

Unity基于粗糙度和金属(Metal/Roughness)工作流
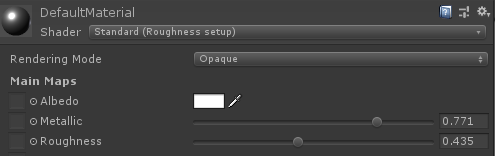

Unity基于高光(Specular/Glossiness )工作流

参考资料
THE PBR GUIDE BY ALLEGORITHMIC - PART 1
THE PBR GUIDE BY ALLEGORITHMIC - PART 2
Siggraph 2014 : Moving Frostbite to Physically based rendering V3