平面投影(Planar Projected Shadows)可以简单理解为点在一个面上交点,注意这个面是没有高度起伏变化的,是平面。观察手游《王者荣耀》为了简化计算也是采用的平面投影,整个战斗场景地面其实在一个平面上。
向量定义
v向量 = d长度 * v方向 = $ d \frac{\vec v}{\vert \vec v \vert} $
向量方程
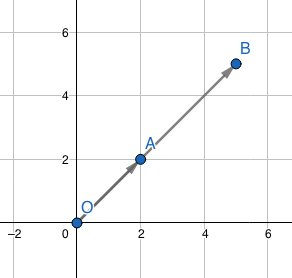
向量方程r描述经过A和B的线,r = OA + dAB,d是标量。如果a是向量OA,b是向量OB,则r = a + d(b - a)。
平面方程
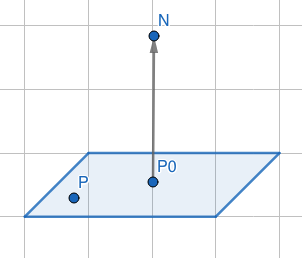
P0是平面上一个点,PO到P绘制的向量和法线N垂直,那么向量点积公式(P-P0)· N = 0 可描述平面上所有点P。
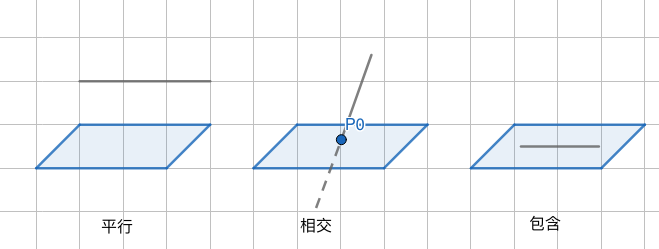
线和平面关系
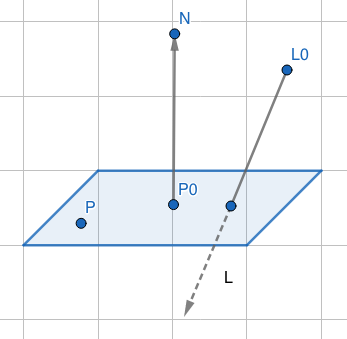
求线和平面交点方法一
-
平面方程:(P-P0)· N = 0 ,N是法线,P0是平面上一点。
-
向量:P = dL + L0 , d是标量长度,L是方向矢量。
-
带入二式计算:
(dL + L0 - P0)· N = 0
dL· N + L0· N - P0· N = 0
\[d = \frac{(P0-L0)· N}{L· N}\]则有:
-
当L· N = 0 时,线和平面平行
-
当(P0-L0)· N = 0时,线包含在平面中,线上所有点都和平面相交
-
当L· N != 0是,一个点和平面相交,该点为 dL + L0。
float3 ShadowProjectPos1(float4 vertPos)
{
float3 shadowPos;
//得到顶点的世界空间坐标
float3 worldPos = mul(unity_ObjectToWorld , vertPos).xyz;
//灯光方向
float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
float3 p0 = float3(0,0,0);
float3 normal = float3(0,1,0);
float distance = dot(p0.xyz - worldPos.xyz, normal.xyz) / dot(lightDir, normal.xyz);
shadowPos.xyz = worldPos.xyz + distance * lightDir;
return shadowPos;
}
求线和平面交点方法二
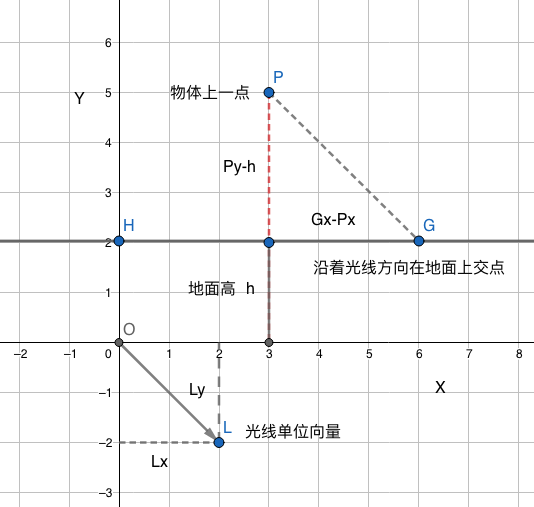
物体上一点P沿光线方向在地面高h上有一个交点G,G则为投影点。
根据三角相似定理
-Ly / Lx = (Py - h) / (Gx - Px)
则投影点G为
Gx = Px - (Lx(Py - h)/Ly)
Gy = h
float3 ShadowProjectPos2(float4 vertPos)
{
float3 shadowPos;
//得到顶点的世界空间坐标
float3 worldPos = mul(unity_ObjectToWorld , vertPos).xyz;
//灯光方向
float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
_Height = 0.1;
//阴影的世界空间坐标(低于地面的部分不做改变)
shadowPos.y = min(worldPos .y ,_Height);
shadowPos.xz = worldPos .xz - lightDir.xz * max(0 , worldPos .y - _Height) / lightDir.y;
return shadowPos;
}
渲染效果如下图
