Unity

渲染和光照

简单介绍光照

Posted by Bob on November 22, 2018

所有我们能看到的东西都是需要进行渲染的。

渲染路径

1.前向渲染（Forward Rendering）

ForwardRendering核心伪代码:


For each light:
    For each object affected by the light:
        framebuffer += object * light
  • Unity将各种光照按逐像素处理（per-pixel）、逐顶点处理（per-vertex）、球谐函数（Spherical Harmonics ）按远近、范围、重要程度、个数等因素分类计算出并混合。
  • 场景中有M个物体，N个光源。 那么理论上进行的光照计算次数为 M*N
2.延迟渲染（Deferred Rendering）

Deferred Rendering核心伪代码:


For each object: 
    Render to multiple targets 
For each light: 
    Apply light as a 2D postprocess
  • 在Pass1中，不进行任何光照计算，而仅仅计算哪些片元是可见的，通过深度缓冲技术，如果发现可见，则把它的相关信息存储到G-Buffer中。
  • 在Pass2中，由G-Buffer中的各种信息来进行真正的光照计算。
  • 场景中有M个物体，N个光源。 那么理论上进行的光照计算次数为 M+N。它先将摄像机空间的点光栅化转化成屏幕坐标后再进行处理。这样就能减少处理的次数，从而提高效率。

色彩空间

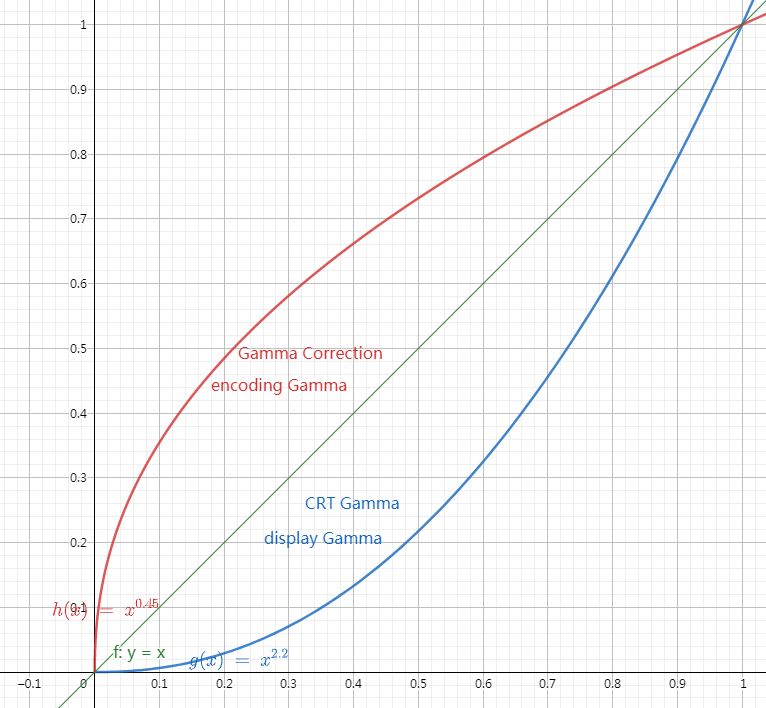
image

  • 图中绿色线描述#000000黑色—>#ffffff白色的线性变化
  • 人眼对暗部的变化更加敏感，比如从0变到0.01的变化。而对亮部变化其实不是很敏感，比如0.99变到1.0。
  • CRT显示器输入电压和显示出来的亮度关系不是线性的，这里的2.2称为 伽马系数(Gamma factor)，范围一般在2.0到2.4之间，不同显示器这个系数有区别。CRT显示器按照非线性方式工作显示亮度减弱会偏暗。gamma值越高，图像越偏暗。
  • 保存颜色信息本身矫正称为encoding gamma，通过pow(1/2.2)将颜色强度提高，上图红线部分。目前大多数互联网和存储在电脑上的图片都是经过0.45伽马校正(Gamma Correction)的。
  • 显示器对颜色的矫正称为display gamma，通过pow(2.2)的操作之后显然会变得更暗，上图蓝线部分。
  • sRGB颜色空间中encoding gamma为0.45，display gamma为2.2。

image

如果你将Gamma0.45叠加到Gamma2.2的显示设备上，便会对偏暗的显示效果做到校正.例如：原始RGB色(0.5,0,0)先Gamma Correction，(0.5,0,0)^0.45 = (0.73,0,0),然后发给显示器(0.73,0,0)^2 = (0.5,0,0),这样就抵消一部分CRT显示器的偏差，正常显示线性颜色了。

1.Linear Color Space

下图是Ps中8位渐变效果（正中间是50%的灰）和Unity线性空间（ OpenGL ES 3支持）渲染

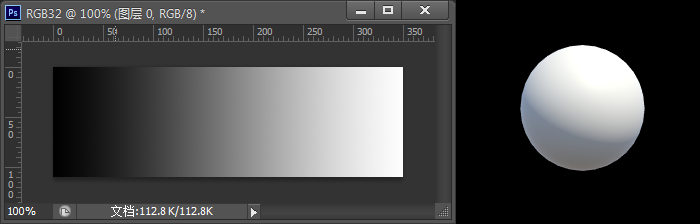
image

使用线性空间的一个显着优点是，随着光强度的增加，提供给场景中着色器的颜色会线性增亮，可确保更精确的渲染。

2.Gamma Color Space

下图是Ps中32位渐变效果（正中间20%的灰）和Unity 伽马空间渲染

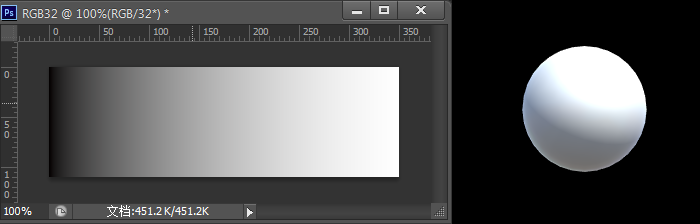
image

注意使用Gamma颜色空间，更多空间存的是更亮的色调。当光强度增加时，颜色如何快速变为白色。

更多详细解释参见文章《了解伽马矫正》

shader转换
unityCG.cginc


// Legacy for compatibility with existing shaders
inline bool IsGammaSpace()
{
    #ifdef UNITY_COLORSPACE_GAMMA
        return true;
    #else
        return false;
    #endif
}
 
inline float GammaToLinearSpaceExact (float value)
{
    if (value <= 0.04045F)
        return value / 12.92F;
    else if (value < 1.0F)
        return pow((value + 0.055F)/1.055F, 2.4F);
    else
        return pow(value, 2.2F);
}
 
inline half3 GammaToLinearSpace (half3 sRGB)
{
    // Approximate version from http://chilliant.blogspot.com.au/2012/08/srgb-approximations-for-hlsl.html?m=1
    return sRGB * (sRGB * (sRGB * 0.305306011h + 0.682171111h) + 0.012522878h);
 
    // Precise version, useful for debugging.
    //return half3(GammaToLinearSpaceExact(sRGB.r), GammaToLinearSpaceExact(sRGB.g), GammaToLinearSpaceExact(sRGB.b));
}
 
inline float LinearToGammaSpaceExact (float value)
{
    if (value <= 0.0F)
        return 0.0F;
    else if (value <= 0.0031308F)
        return 12.92F * value;
    else if (value < 1.0F)
        return 1.055F * pow(value, 0.4166667F) - 0.055F;
    else
        return pow(value, 0.45454545F);
}
 
inline half3 LinearToGammaSpace (half3 linRGB)
{
    linRGB = max(linRGB, half3(0.h, 0.h, 0.h));
    // An almost-perfect approximation from http://chilliant.blogspot.com.au/2012/08/srgb-approximations-for-hlsl.html?m=1
    return max(1.055h * pow(linRGB, 0.416666667h) - 0.055h, 0.h);
 
    // Exact version, useful for debugging.
    //return half3(LinearToGammaSpaceExact(linRGB.r), LinearToGammaSpaceExact(linRGB.g), LinearToGammaSpaceExact(linRGB.b));
}

光源种类

1.环境光(Ambient Lighting)

image

没有光（左）和只有环境光（右）

2.点光源 (Point Lights)

image

模拟灯泡

3.平行光(Directional Lights)

image

模拟阳光

4.聚光灯(Spotlights)

image

模拟路灯

5.区域光(Area Lights)

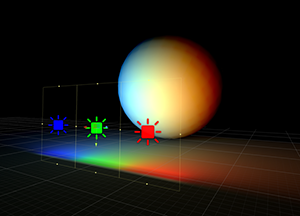
image

光在区域光的表面上发射，产生具有柔和阴影的漫射光。

物理知识

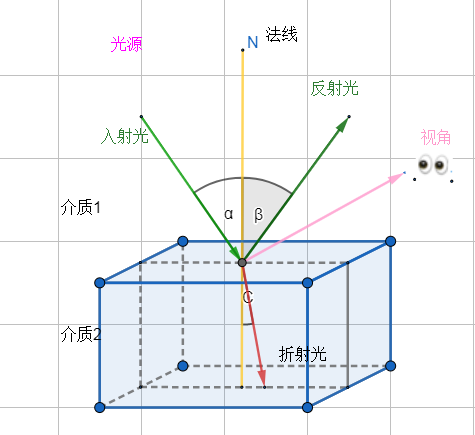
image

  • 反射定律：入射角A等于反射角B，而且反射光线、入射光线与法向量在同一平面上。
  • 折射定律：折射线在入射线与法线构成的平面上，折射角C与入射角A满足如下关系 ：sinA/sinC=介质1折射率/介质2折射率

光照模型要素

能量守恒:入射强度 = 漫反射光强(diffuse) + 镜面反射(specular) + 折射(refraction) + 吸收光强(absorbed)

1.自发光（Emission）

一般指自发光物体或者光源，这种光不受其它光源的影响

2.环境光（Ambient）
  • 环境光被建模为一个没有光源、没有方向并且对场景中的所有物体产生相同的点亮效果的一种光。
  • Ambient 不依赖于光源的方向。

image


//环境光
fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.rgb;
3.漫反射（Diffuse）
  • 光线射到物体表面上后（比如泥塑物体的表面，没有一点镜面效果），光线会沿着不同的方向等量的散射出去，这种现象称为漫反射。漫反射光在不同方向都是一样的 。漫反射光均匀向各方向传播，与视点无关，它是由表面的粗糙不平引起的 。

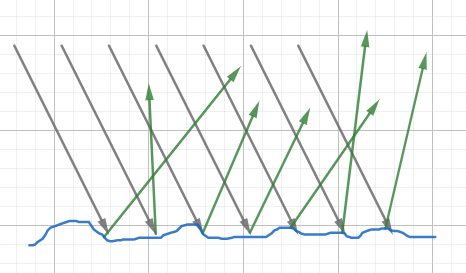
image

  • diffuse 只依赖于光源的方向和法线的方向
4.高光（Specular）
  • 一束光照射到一面镜子上或不绣钢的表面，光线会沿着反射光方向全部反射出去，这种叫镜面反射光。

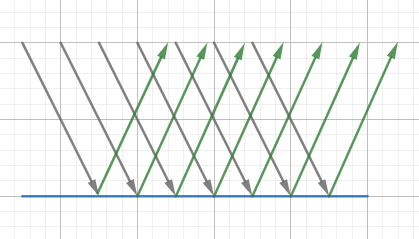
image

  • specular依赖于光源的方向，法线的方向和视角的方向
5.折射

比如水晶、玻璃等，光线会穿过去一直往前走

光照模型

1.Lambert模型

image

  • 光从任何角度射入到物体表面，都会分散的反射出去，且所有方向的光照强度都是相同的。反射光的强度取决于入射光和表面发现的夹角。理想漫反射模型，各个方向一样。

  • Lambert模型较好的表现了粗糙表面的光照现象，如墙壁，纸张等，但是在用于诸如金属等有光泽效果的材质上则会显得呆板，表现不出光泽，主要原因是Lambert光照模型没有考虑表现这些表面的镜面反射（没有视角方向参与）效果。

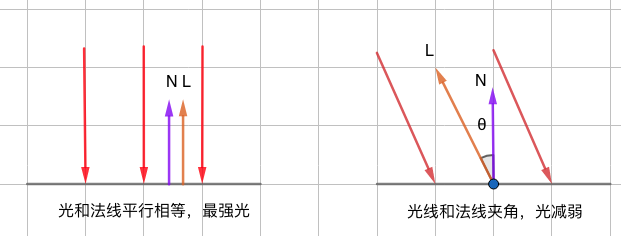
  • l·n = 丨l丨丨n丨cosθ ,如果入射光l和顶点法线n都是单位向量，则它们的点积(dot product) dot(入射光l,顶点法线n)=l·n=cosθ,cosθ则为二个向量的夹角。

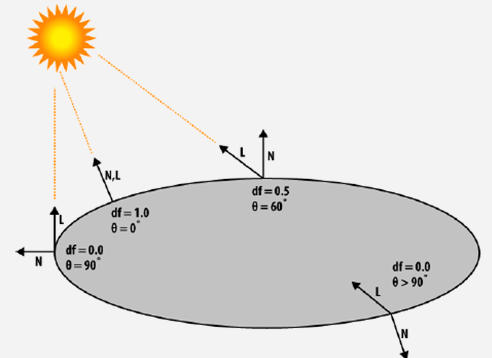
  • 漫反射光 Diffuse = 入射光颜色 * max( 0 , dot(入射光l,法线n))。 入射角为0°时，说明光线垂直于物体表面，漫反射光强最大； 入射角为90°时光线与物体表面平行，物体接收不到任何光线； 入射角为小于0°的被截止掉，物体后面不被照亮。

image


//v.normal : 将模型空间下的顶点法线填充normal 

//法线的单位向量

fixed3 normalDir=normalize(mul(v.normal,(float3x3)unity_WorldToObject));

//入射光的向量

fixed3 lightDir=normalize(_WorldSpaceLightPos0.xyz);

//漫反射的颜色，一般这步采用逐像素处理，比逐顶点更平滑一些

fixed3 diffuse =_LightColor0.rgb*max(dot(normalDir,lightDir),0);

//HalfLambert ，提亮物体

fixed3 halfDiffuse = diffuse*0.5+0.5;

//反射光方向

fixed3 reflectDir = normalize(reflect(-lightDir, normalDir));
2.Blinn-Phong & Phong（冯氏光照模型）
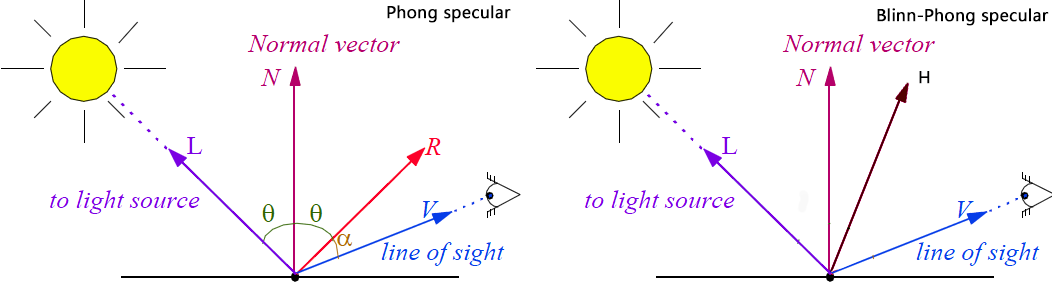
  • 光线照射在光滑物体表面后，在特定方向上会有很强的反射，即发生全反射(镜面发射)。全反射光主要集中在一个近似圆锥角的范围内.n为法线，l为光线入射方向（从光指向顶点），r为全反射方向，E为观察点，因此v为视角方向。全反射光进入眼睛的强度与v和r的角度θ有关，随着该角度增大，全反射光照强度下降。离主反射光线方向越近的方向，反射光照强度越强。

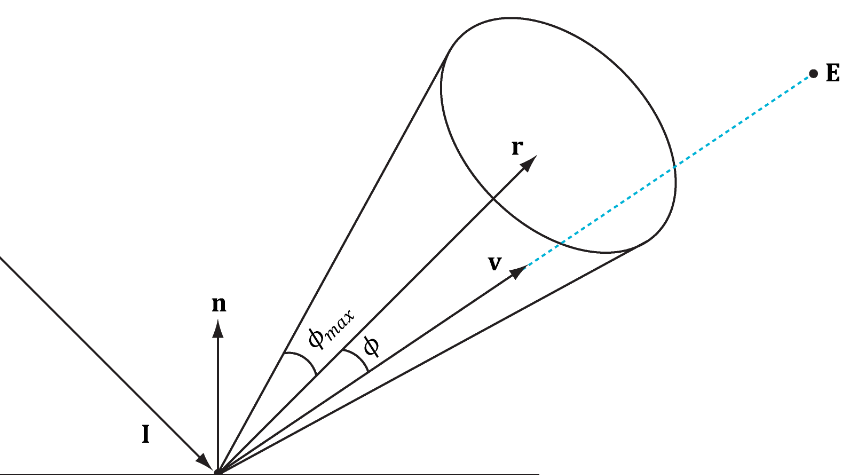
image

下面是二种模型的具体公式，L是入射光从顶点指向光，N是顶点法线，R是反射光，V是顶点指向眼睛观察方向，H是L和V夹角二分之一方向定义为反射方向，简化Phong的反射计算。

  • 反射光R = L - 2(N·L)*N （反射向量推导见文章《常见数学公式》文末）

  • Phong高光亮度 = dot(视角方向V,反射光R)^高光系数*入射光颜色

  • 反射光H = normalize(入射光方向+视角方向)

  • Blinn-Phong高光亮度 = max(dot(法线方向,反射光H),0)^高光系数*入射光颜色

image


//v.position：将模型空间下的位置坐标填充给position,

float4 position = mul(UNITY_MATRIX_MVP,v.position);

// 视野方向

fixed3 viewDir = normalize(_WorldSpaceCameraPos.xyz - mul(position , unity_WorldToObject).xyz);

//得到平行光和视野方向的平分线

fixed3 halfDir = normalize(lightDir+viewDir);

//得到高光反射 Blinn-Phong

fixed3 specular = _LightColor0.rgb * pow(max(dot(normalDir,halfDir),0),_Gloss);

高光具体实例见文章《角色光照》

ADS光照模型

image 上图来自gamedev

LightIntensity = Ambient + Diffuse + Specular;

CATALOG
    FEATURED TAGS
    Lua Unity HardWare C++ C#
    FRIENDS