图形学中会用到的比较基础的3D数学,重点在线性代数知识。
所有图形均采用GeoGebra绘制。
余弦定理
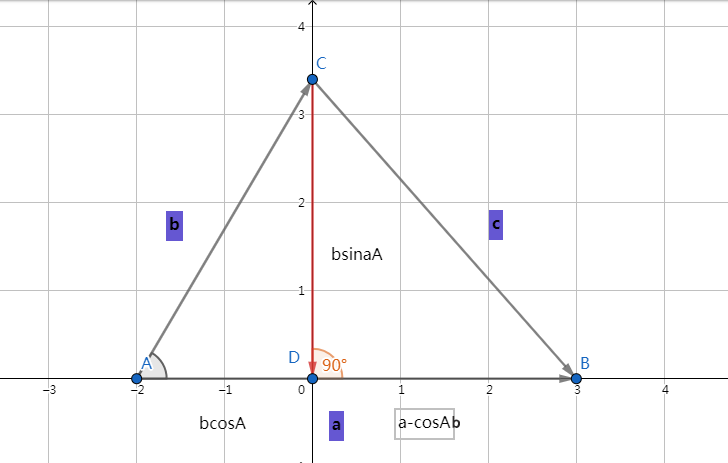
在三角形中ABC中,已知AB=a,AC=b,CB=c,cd⊥ab, cd=bsinA,bd=a-bcosA。
勾股定理c² = cd² + bd²
c² = (bsinA)² + (a-bcosA)²
c² = b²sinA² + a² + b²cosA² - 2abcosA
因sinA² + cosA² = 1
c² = b² + a² - 2abcosA
注意这里计算是标量!!!
标量(scalar)
游戏中一般用标量描述时间、质量、面积、体积、长度、距离、速度、角度等。
向量(Vector)
向量,又称矢量。向量表示的是方向和大小,与位置距离无关
点可表示为位置矢量(position vector)、径向量(radius vector)
在unity3d中采用的struct来描述的Vector3
namespace UnityEngine
{
public struct Vector3
{
public float x;
public float y;
public float z;
}
}
向量加减法
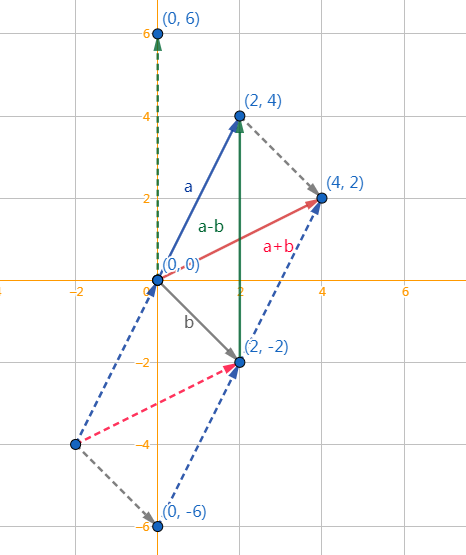
a(2,4) + b(2,-2) = (2+2,4-2) = (4,2)
b(2,-2) + a(2,4) = (2+2,-2+4) = (4,2)
加法:飞机通过马达动力的位移(a)、风影响的位移(b),计算真正的位移c
a(2,4)-b(2,-2) = (2-2,4-(-2)) = (0,6)
a(2,4)+(-b(2,-2)) = (2,4) + (-2,2) = (0,6)
减法:角色从b点到a点的位移
向量只有模和方向二个属性,没有位置信息,虚线就是平移后向量。图中同种颜色虚实是同一个向量
在unity3d中向量加法
public static Vector3 operator +(Vector3 a, Vector3 b)
{
return new Vector3(a.x + b.x, a.y + b.y, a.z + b.z);
}
在unity3d中向量减法
public static Vector3 operator -(Vector3 a, Vector3 b)
{
return new Vector3(a.x - b.x, a.y - b.y, a.z - b.z);
}
| 运算 | 结果 | 意义 |
|---|---|---|
| vector + vector | vector | 叠加 (x1,y1,0) + (x2,y2,0) = (x1+x2,y1+y2,0) 结果中w=0,依旧为一个向量 |
| vector - vector | vector | 叠加反向vector |
| point + vector | point | 把点平移 (x1,y1,1) + (x2,y2,0) = (x1-x2,y1-y2,1) 结果中w=1,依旧为一个点 |
| point - vector | point | 把点平移 |
| point - point | vector | 二点之间距离或方向 (x1,y1,1) - (x2,y2,1) = (x1-x2,y1-y2,0) 结果中w=0,变为一个向量 |
| point + point | —— | 无意义 (x1,y1,1) + (x2,y2,1) = (x1+x2,y1+y2,2) 结果中w=2,无意义(实际上等于两点的中点,即 ((x1+x2)/2,(y1+y2)/2) ) |
向量和标量的乘法和除法
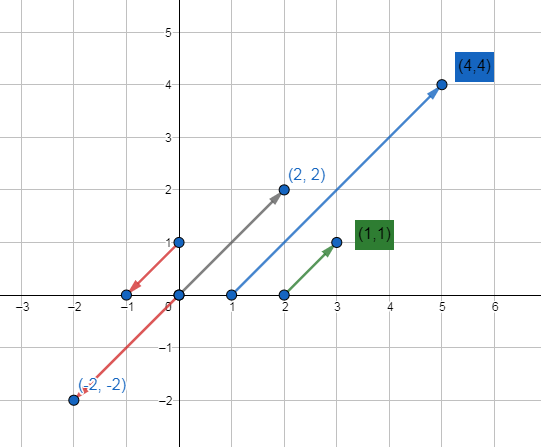
向量变负,将得到一个和原来向量大小相等,方向相反的向量
a(2,2) * -1 = a(2 * -1,2 * -1) = (-2,-2)
a(2,2) * 2 = a(2 * 2,2 * 2) = (4,4)
a(2,2) / 2 = a(2 / 2,2 / 2) = (1,1)
数乘向量:实数λ与向量b的积是一个向量,记作:a=λb。规定:当λ为正时,同向;当λ为负时,反向;实数λ,叫做向量的系数。数乘向量的几何意义就是把向量沿着相同方向或反方向放大或缩小
public static Vector3 operator *(Vector3 a, float d)
{
return new Vector3(a.x * d, a.y * d, a.z * d);
}
public static Vector3 operator *(float d, Vector3 a)
{
return new Vector3(a.x * d, a.y * d, a.z * d);
}
向量的模
向量的模是个标量,表示在空间中的长度。
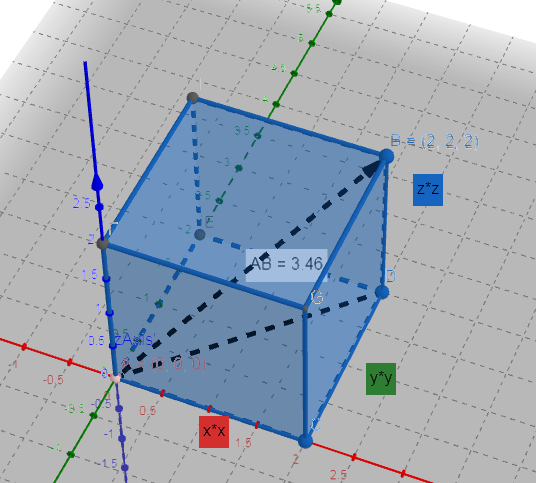
空间向量v(x,y,z),其中x,y,z分别是三轴上的坐标,模长是:
丨v丨 = sqrt(x²+y²+z²)
丨v丨= sqrt(2²+2²+2²) = 3.464
也可记‖v‖ = 3.464
在unity3d中求模
public float magnitude
{
get
{
return Mathf.Sqrt(this.x * this.x + this.y * this.y + this.z * this.z);
}
}
//不开方
public float sqrMagnitude
{
get
{
return this.x * this.x + this.y * this.y + this.z * this.z;
}
}
三维空间中两点的距离
public static float Distance(Vector3 a, Vector3 b)
{
Vector3 vector = new Vector3(a.x - b.x, a.y - b.y, a.z - b.z);
return Mathf.Sqrt(vector.x * vector.x + vector.y * vector.y + vector.z * vector.z);
}
向量比较
在unity中向量比较是判断模
public static bool operator ==(Vector3 lhs, Vector3 rhs)
{
return Vector3.SqrMagnitude(lhs - rhs) < 9.99999944E-11f;
}
public static bool operator !=(Vector3 lhs, Vector3 rhs)
{
return Vector3.SqrMagnitude(lhs - rhs) >= 9.99999944E-11f;
}
单位向量
向量的规范化也称(归一化)就是使向量的模变为1,即变为单位向量
在计算光照时候需要知道顶点的法线方向和光照方向,而不关心长度。归一化normalized 就是把向量转为单位向量(方向不变,长度变为1)。一个非0的向量v, v的单位向量为v/丨v丨,如果丨v丨 = 1,则向量v{x,y,z}称为单位向量。
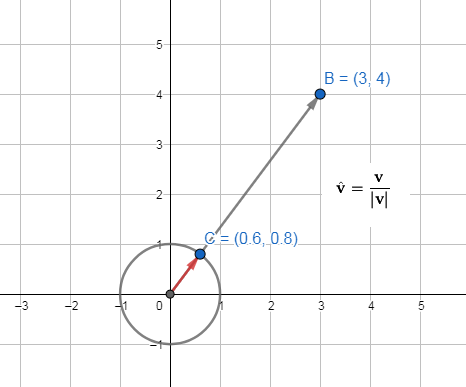
v的单位向量=(3,4)/丨(3,4)丨=(3,4)/sqrt(3²+4²)=(3/5,4/5)=(0.6,0.8)
上图红色的向量就是规范化后的向量,v上面的倒三角读作v roof
在unity中规范化向量
public static Vector3 Normalize(Vector3 value)
{
float num = Vector3.Magnitude(value);
if (num > 1E-05f)
{
return value / num;
}
return Vector3.zero;
}
向量点积(dot product,inner product)
向量点乘(内积)是其各个分量乘积的和
a·b = (ax,ay)·(bx,by) = axbx+ayby
满足交换律,注意这里的·符号乘不是标量的乘。
a·b = b·a
a·b = 0,a⊥b
a·a = 0,a = 0
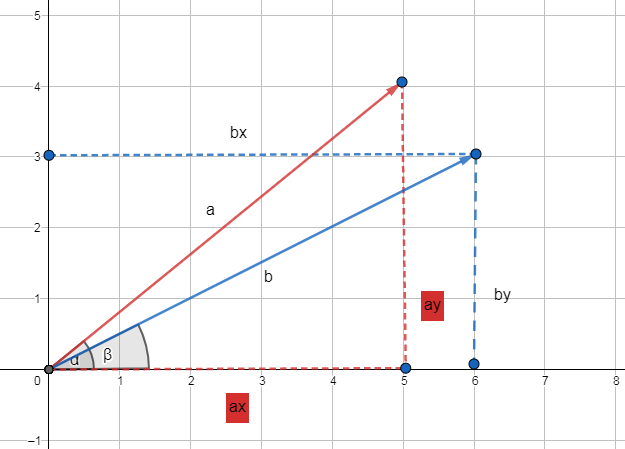
点乘的几何意义:计算两个向量之间的夹角
a·b = 丨a丨丨b丨cosθ
推导方式一如下: a·b = axbx+ayby
a·b = (丨a丨sinA)(丨b丨sinB) + (丨a丨cosA)(丨b丨cosB)
a·b = 丨a丨丨b丨(sinAsinB + cosAcosB)
a·b = 丨a丨丨b丨cos(A-B)
a·b = 丨a丨丨b丨cosθ
cosθ = (a·b)/(丨a丨丨b丨)
θ = arccos ((a·b)/(丨a丨丨b丨))
设a(1,0)和b(0,1)都是单位向量,a·b = cosθ,这样我们就可判断这两个向量是否是同一方向。
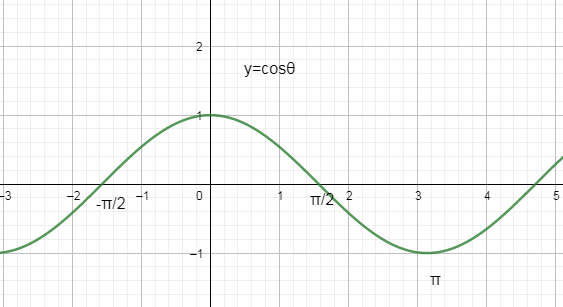
上图是cos函数,π等于180° 。
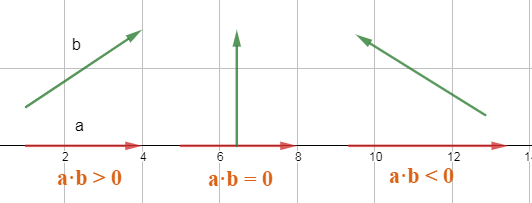
a·b>0 方向基本相同,夹角在0°到90°之间
a·b=0 正交,相互垂直
a·b<0 方向基本相反,夹角在90°到180°之间
之前文章角色光照就用到了dot product,视角方向和法向夹角相互垂直时就是角色边缘。
在unity3d中求点积
public static float Dot(Vector3 lhs, Vector3 rhs)
{
return lhs.x * rhs.x + lhs.y * rhs.y + lhs.z * rhs.z;
}
两个向量之间的弧度
public static float AngleBetween(Vector3 from, Vector3 to)
{
return Mathf.Acos(Mathf.Clamp(Vector3.Dot(from.normalized, to.normalized), -1f, 1f));
}
两个向量之间的角度
public static float Angle(Vector3 from, Vector3 to)
{
return Mathf.Acos(Mathf.Clamp(Vector3.Dot(from.normalized, to.normalized), -1f, 1f)) * 57.29578f;//角度
}
大多数旋转函数需要用弧度制的角:
角度制,就是用角的大小来度量角的大小的方法。在角度制中,我们把周角的1/360看作1度,那么,半周就是180度,一周就是360度。由于1度的大小不因为圆的大小而改变,所以角度大小是一个与圆的半径无关的量,记为degree。
弧度制,顾名思义,就是用弧的长度来度量角的大小的方法。单位弧度定义为圆周上长度等于半径的圆弧与圆心构成的角。记为rad。
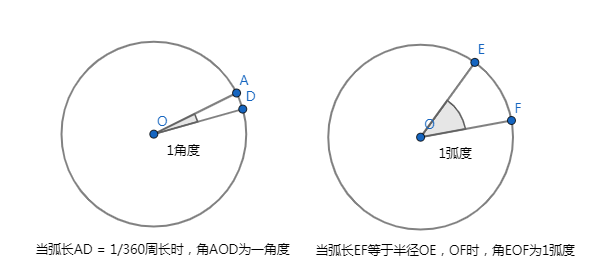
圆的周长(r半径)为2πr,圆一周弧长等于周长为:2πr ,根据:弧度 = 弧长 / 半径,圆一周的弧度为:2πr/r = 2π,根据圆为360 º,弧度为2π,即 360º = 2π 。
弧度转角度:
1弧度 = 360/2π = 180 / π
角度 = 弧度 * (180 / π)
角度转弧度:
1角度 = 2π/360 = π / 180
弧度 = 角度 * (π / 180)
判断目标在自己的前后方位可以使用下面的方法:
Vector3.Dot(transform.forward, target.position)
返回值为正时,目标在自己的前方,反之在自己的后方
点乘的几何意义:投影
AD向量为在b向量在a向量方向上的投影
AD长度 = 丨b丨cosθ
AD向量 = AD长度Xa的方向 = AD长度X(a/丨a丨)
AD向量 = (a丨b丨cosθ)/丨a丨 = (a丨b丨/丨a丨)((a·b)/(丨a丨丨b丨))
AD向量 = (a·b) * a / 丨a丨²
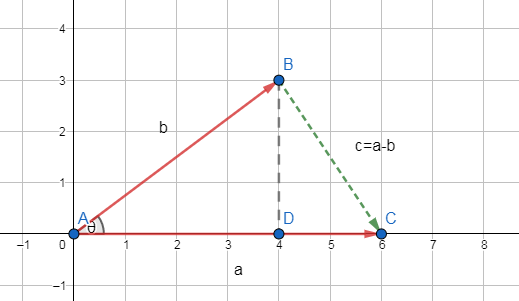
在unity中求投影
public static Vector3 Project(Vector3 vector, Vector3 onNormal)
{
float num = Vector3.Dot(onNormal, onNormal);
if (num < 1.17549435E-38f)
{
return Vector3.zero;
}
return onNormal * Vector3.Dot(vector, onNormal) / num;
}
推导方式二如下,根据余弦定理也可推导:
a(ax,ay)、b(bx,by)、c(ax-bx,ay-by)表示向量,a向量和b向量夹角为θ。
丨c丨² = 丨a丨²+丨b丨²-2丨a丨丨b丨cosθ
丨a丨丨b丨cosθ = (丨a丨²+丨b丨²-c²)/2
丨a丨丨b丨cosθ = (ax²+ay²+bx²+by²-((ax-bx)²+(ay-by)²)/2
丨a丨丨b丨cosθ = axbx+ ayby
丨a丨丨b丨cosθ = a·b
推导方式三如下
丨c丨² = 丨a丨²+丨b丨²-2丨a丨丨b丨cosθ
c = a-b
一个向量和本身的点积是该向量模的平方
c·c= cxcx + cycy + czcz = 丨c丨²
丨c丨² = 丨a-b 丨² = (a - b)·(a - b) = 丨a丨²+丨b丨²-2(a·b)
丨a丨²+丨b丨²-2(a·b) = 丨a丨²+丨b丨²-2丨a丨丨b丨cosθ
a·b = 丨a丨丨b丨cosθ
其他性质:
如果(a+b)·(a-b) = 0,可推导出丨a丨= 丨b丨
交换律:a·b = b·a
分配律: a·(b + c) = a·b + a·c
结合律: (ma)·b = m(a·b) = a·(mb) m是实数
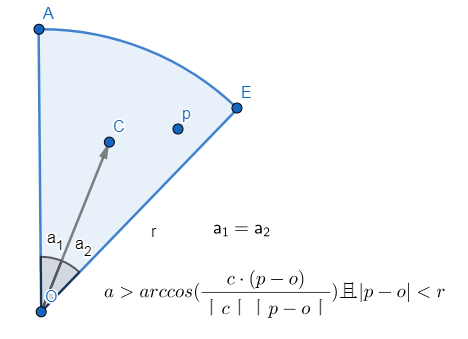
点乘的使用:点p是否在扇形内
向量叉积(cross product,outer product)
叉乘(外积、向量积)计算公式如下:
aXb = (ax,ay,az)X(bx,by,bz)=(aybz-azby,azbx-axbz,axby-aybx)
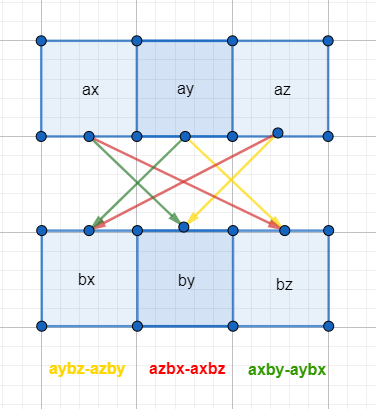
这个公式不好记,用划掉所在行列维度(余子式(Minor))就容易记了,红色就是划掉,注意第二个列j符号是负的。

叉乘的几何意义:法向量
向量a和向量b的叉乘结果是一个向量,一般用于法向量,该向量垂直于a和b向量构成的平面
叉积用右手法则可以确定叉乘积的方向。不满足交换律axb ≠ bxa,而满足反交换律axb = - bxa。可以使用叉积的正负值来判断向量a,b的相对位置,即向量b是处于向量a的顺时针方向还是逆时针方向
在unity3d中计算:(注意在Unity中使用左手坐标系,用左手法则来判断。)
Debug.Log(Vector3.Cross(new Vector3(1,0,2),new Vector3(2,0,1)));
a(1,0,2) X b(2,0,1) = (0.0,3.0, 0.0) b在a的顺时针方向
a’(-1,0,-2) X b(2,0,1) = (0.0,-3.0, 0.0) b在a的逆时针方向
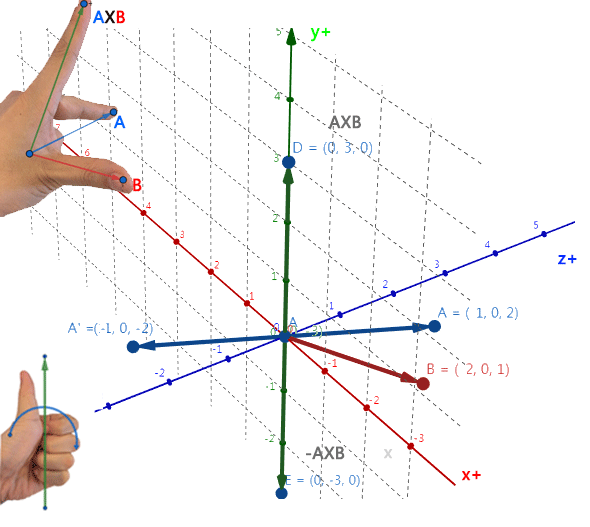
简单的说: 点乘判断角度,叉乘判断方向
在Unity中(左手坐标系)判断目标在自己的左右方位可以使用下面的方法:
Vector3.Cross(transform.forward, target.position).y
返回值为正时,目标在自己的右方,反之在自己的左方
叉乘的几何意义也是等于由两个向量为边组成的平行四边形的面积。
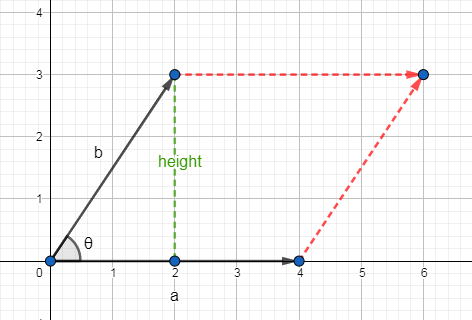
面积 = 丨a丨 * height = 丨a丨 * 丨b丨sinθ
向量a和向量b的叉乘结果是一个向量,这个向量的长度恰好等于面积。
| aXb | = 丨a丨丨b丨sinθ |
其他性质:
反交换律:aXb = -bXa
分配律:ax(b+c) = aXb + aXc
结合律: (ma)Xb = aX(mb) = m(aXb) m是实数
非零向量a和b平行有aXb = 0
反射向量
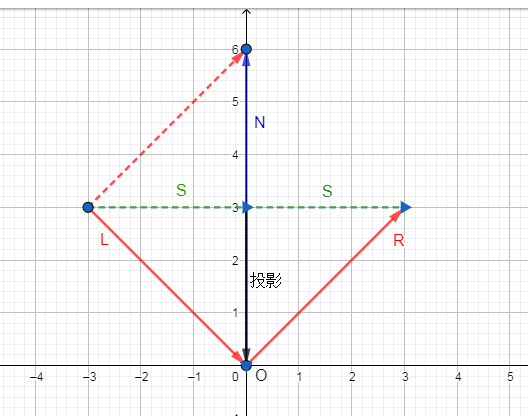
L光线向量(从光指到顶点)、N法向量,推导R反射向量
R=2S-L
设N和L的都是单位向量,丨N丨 = 1
L在N上的投影是 = (N·L) * N / 丨N丨² = (N·L)*N
S = L - 投影
R = 2(L-投影)-L
R = L - 2投影
R = L - 2(N·L)*N
在unity中求反射向量
public static Vector3 Reflect(Vector3 inDirection, Vector3 inNormal)
{
return -2f * Vector3.Dot(inNormal, inDirection) * inNormal + inDirection;
}
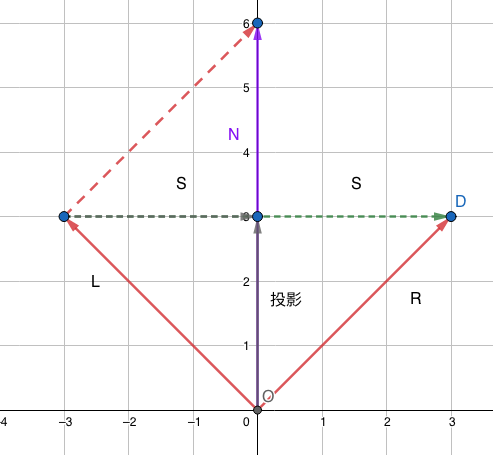
如果L光线向量是从顶点指到光
R = 2S+L
S = 投影 - L
R = 2(投影-L)+L
R = 2投影 - L
R = 2(N·L)*N - L
参考资料: